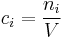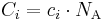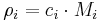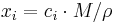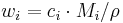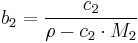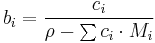Molar concentration

In chemistry, the molar concentration, 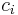$c_i$ is defined as the amount of a constituent 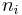$n_i$ divided by the volume of the mixture $V$ ^[1]:

$c_i = \frac {n_i}{V}$

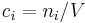It is also called molarity, amount-of-substance concentration, amount concentration, substance concentration, or simply concentration. The volume $V$ in the definition $c_i = n_i/V$ refers to the volume of the solution, not the volume of the solvent. One litre of a solution usually contains either slightly more or slightly less than 1 litre of solvent because the process of dissolution causes volume of liquid to increase or decrease.

1 Units
2 Related Quantities
3 Properties
- 3.1 Dependence on volume
4 Examples
5 References
6 External links

Units

The SI-unit is mol/m³. However, more commonly the unit mol/L is used. A solution of concentration 1 mol/L is also denoted as "1 molar" (1 M).

1 mol/L = 1 mol/dm³ = 1 mol dm⁻³ = 1 M = 1000 mol/m³.

An SI prefix is often used to denote concentrations. Commonly used units are listed in the table below:

Name	Abbreviation	Concentration	Concentration (SI-unit)
millimolar	mM	10⁻³ mol/dm³	10⁰ mol/m³
micromolar	μM	10⁻⁶ mol/dm³	10⁻³ mol/m³
nanomolar	nM	10⁻⁹ mol/dm³	10⁻⁶ mol/m³
picomolar	pM	10⁻¹² mol/dm³	10⁻⁹ mol/m³
femtomolar	fM	10⁻¹⁵ mol/dm³	10⁻¹² mol/m³
attomolar	aM	10⁻¹⁸ mol/dm³	10⁻¹⁵ mol/m³
zeptomolar	zM	10⁻²¹ mol/dm³	10⁻¹⁸ mol/m³
yoctomolar	yM^[2]	10⁻²⁴ mol/dm³ (1 molecule per 1.6 L)	10⁻²¹ mol/m³

Related Quantities

Number concentration

The conversion to number concentration 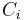$C_i$ is given by:

$C_i = c_i \cdot N_{\rm A}$

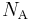where $N_{\rm A}$ is the Avogadro constant, approximately 6.022×10²³ mol⁻¹.

Mass concentration

The conversion to mass concentration 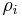$\rho_i$ is given by:

$\rho_i = c_i \cdot M_i$

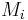where $M_i$ is the molar mass of constituent $i$ .

Mole fraction

The conversion to mole fraction $x_i$ is given by:

$x_i = c_i \cdot M / \rho$

where $M$ is the average molar mass of the solution and $\rho$ is the density of the solution.

Mass fraction

The conversion to mass fraction 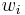$w_i$ is given by:

$w_i = c_i \cdot M_i / \rho$

Molality

The conversion to molality (for binary mixtures) is:

$b_2 = \frac{{c_2}}{{\rho - c_2 \cdot M_2}} \,$

where the solute is assigned the subscript 2.

For solutions with more than one solute, the conversion is:

$b_i = \frac{{c_i}}{{\rho - \sum c_i \cdot M_i}} \,$

Properties

Dependence on volume

Molar concentration depends on the variation of the volume of the solution due mainly to thermal expansion.

Examples

Example 1: Consider 11.6 g of NaCl dissolved in 100 g of water. The final mass concentration $\rho$ (NaCl) will be:

$\rho$ (NaCl) = 11.6 g / (11.6 g + 100 g) = 0.104 g/g = 10.4 %

The density of such a solution is 1.07 g/mL, thus its volume will be:

$V$ = (11.6 g + 100 g) / (1.07 g/mL) = 104.3 mL

The molar concentration of NaCl in the solution is therefore:

$c$ (NaCl) = 11.6 g / (58 g/mol * 104.3 mL) = 0.00192 mol/mL = 1.92 mol/L

Here, 58 g/mol is the molar mass of NaCl.

Example 2: Another typical task in chemistry is the preparation of 100 mL (= 0.1 L) of a 2 mol/L solution of NaCl in water. The mass of salt needed is:

$m$ (NaCl) = 2 mol/L * 0.1 L * 58 g/mol = 11.6 g

To create the solution, 11.6 g NaCl are placed in a volumetric flask, dissolved in some water, then followed by the addition of more water until the total volume reaches 100 mL.

Example 3: The density of water is approximately 1000 g/L and its molar mass is 18.02 g/mol. Therefore, the molar concentration of water is:

$c$ (H₂O) = 1000 g/L / (18.02 g/mol) = 55.5 mol/L

Likewise, the concentration of solid hydrogen (molar mass = 2.02 g/mol) is:

$c$ (H₂) = 88 g/L / (2.02 g/mol) = 43.7 mol/L

The concentration of pure osmium tetroxide (molar mass = 254.23 g/mol) is:

$c$ (OsO₄) = 5.1 kg/L / (254.23 g/mol) = 20.1 mol/L.

Example 4: Proteins in bacteria, such as E. coli, usually occur at about 60 copies, and the volume of a bacterium is about 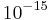$10^{-15}$ L. Thus, the number concentration $C$ is:

$C$ = 60 / (10⁻¹⁵ L)= 6×10¹⁶ L⁻¹

The molar concentration is:

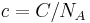$c = C / N_A$ = 6×10¹⁶ L⁻¹ / (6×10²³ mol⁻¹) = 10⁻⁷ mol/L = 100 nmol/L

If the concentration refers to original chemical formula in solution, the molar concentration is sometimes called formal concentration. For example, if a sodium carbonate solution has a formal concentration of $c$ (Na₂CO₃) = 1 mol/L, the molar concentrations are $c$ (Na⁺) = 2 mol/L and $c$ (CO₃^2-) = 1 mol/L because the salt dissociates into these ions.

References

^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "amount concentration, c".
^ David Bradley. "How low can you go? The Y to Y". http://www.sciencebase.com/yocto.html.

External links

Articles related to solutions

Solution	Ideal solution · Aqueous solution · Solid solution · Buffer solution · Flory-Huggins · Mixture · Suspension · Colloid · Phase diagram · Eutectic point · Alloy · Saturation · Supersaturation · Serial dilution · Dilution (equation) · Apparent molar property

Concentration and related quantities	Molar concentration · Mass concentration · Number concentration · Volume concentration · Normality · Percentage solution · Molality · Mole fraction · Mass fraction · Mixing ratio

Solubility	Solubility equilibrium · Total dissolved solids · Solvation · Solvation shell · Enthalpy of solution · Lattice energy · Raoult's law · Henry's law · Solubility table (data) · Solubility chart

Solvent	(category) · Acid dissociation constant · Protic solvent · Inorganic nonaqueous solvent · Solvation · List of boiling and freezing information of solvents Partition coefficient · Polarity · Hydrophobe · Hydrophile · Lipophilic · Amphiphile